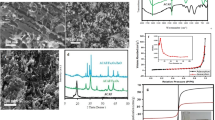
Abstract
Chloroquine has been reported as an effective drug for the treatment of COVID-19 and with the rise in its administration and continued use, metabolites of chloroquine invariably find their way into the environment. There are many concerns recently on the presence of pharmaceuticals in the aquatic environment, hence the need for environmental remediation via effective adsorbent. Plantain peel activated carbon-supported zinc oxide (PPAC-ZnO) nanocomposite was prepared and characterized using physicochemical and spectroscopic techniques. The rate of uptake of chloroquine by PPAC-ZnO nanocomposite was investigated by batch technique under different operational parameters. PPAC-ZnO nanocomposite was characterized by various physicochemical techniques by SBET = 606.07 m2g−1, pH(pzc) = 4.98 surface area by Saer’s method = 273.4 m2g−1. The carboxylic, phenols, lactone, and basic sites were determined by the Boehm method. Chloroquine uptake was confirmed by FTIR and SEM before and after adsorption. Change in morphology after adsorption was revealed by scanning electron microscopy (SEM). X-ray diffraction (XRD) showed the crystallinity of PPAC-ZnO nanocomposite. The batch adsorption experiment results showed that adsorption capacity increased with an increase in temperature. The maximum chloroquine sorption was 78.89% at a concentration of 10 ppm and a temperature of 313 K. Equilibrium sorption fitted well to Langmuir and Temkin isotherms with a high correlation coefficient (R2) of 0.99. Pseudo-second-order best described the kinetic data and adsorption mechanism was pore diffusion dependent. Thermodynamics parameters (ΔG = − 25.65 to − 28.79 kJmol−1; ΔH = 22.06 kJmol−1 and ΔS = 157.69 Jmol−1) demonstrated feasibility, spontaneity, and endothermic behavior of the process with degrees of randomness. The activation energy for adsorption was less than 40 kJmol−1 suggesting a physisorption mechanism. This study results revealed that PPAC-ZnO nanocomposites are a sustainable and effective adsorbent for the removal of pharmaceutical waste.
Graphical abstract

Similar content being viewed by others
1 Introduction
The first ever reported case of Coronavirus disease popularly known as COVID-19 was in Wuhan China in December 2019. This disease is characterized by cough, smell and taste loss, tiredness, nasal congestion, etc. Generally, the symptoms are similar to pneumonia. In January 2020, however, the outbreak was announced as a pandemic by the WHO. Ever since then, various research groups have sought for a remedy for this outbreak, and on the basis of clinical research, chloroquine (CQ) and hydroxychloroquine (HCQ) have been identified as potent drugs for the control of COVID-19. CQ is a drug popularly used for the treatment of malaria and other diseases like rheumatoid arthritis, Q fever [1], lupus erythematosus [2], and photosensitive diseases [3]. Most recently, its application in the control of COVID -19 has caused a rise in demand for the drug although its effectiveness is questioned by many studies [4, 5]. Its application for the treatment of various diseases and continued use for such purposes have led to a rise in the production of chloroquine and as such an increase in the amount present in wastewater. CQ can enter the environment and invariably natural water bodies through excretion. Reports show that the main route of excretion of CQ is renal with about 23–25% excreted in its unmodified form [6]. Also, through effluent and waste disposal from hospitals and pharmaceutical industries, leaching from dumpsites and run-off can occur from improper disposal of unused CQ drugs [7]. As a result of its chemical structure (Fig. 1) and physical and chemical properties, CQ persists in the environment (air, land, and water bodies) and as such can contaminate, bioaccumulate, and be transferred to living organisms in toxic forms [2]. The high solubility, low biodegradation of CQ has raised various concerns about CQ as an emerging contaminant. Also, the N atom embedded in the quinoline cyclic structure makes chloroquine hydrophilic and as such increases its prevalence in the aquatic environment [2].
Recent studies focus more on the photodegradation and photochemical stability of CQ and HCQ in aqueous solutions. To the best of our knowledge, no reported studies were found on the adsorption of chloroquine from aqueous solutions. The abiotic degradation of HCQ by sunlight photolysis was monitored by Dabi et al. [3] using NMR and HPLC. However, due to the high toxicity and resistance of the degraded products, there is a need to investigate effective methods of removal of CQ micropollutants from wastewater before they are introduced to natural water bodies. Adsorption, which is the process whereby molecules adhere to the surface of an adsorbent, is a technique that has shown high efficiency for the uptake of pollutants [8]. Although various adsorbents have been applied for the uptake of pollutants ranging from biochar’s, zeolites, clay, etc., the activated carbon has however been found to be an effective adsorbent for the uptake of inorganic and organic micropollutants [9]. Low-cost materials have also been extensively studied as alternative adsorbents for pharmaceuticals and recent studies have shown that banana stalk [10], corn cob and sugarcane bagasse [11], rice husk [12], argan tree nutshell [13], etc. could be used effectively as adsorbents. Plantain peels are effective as good adsorbents and have been effectively applied for lead (II) and 3,7- bis(dimethylamino)-phenothiazin-5-ium chloride adsorption [14], pesticides [15], rhodamine B dyes [16], and 2–6,dichlorophenol [17]. The disposal of plantain waste could pose a threat to the environment as they clog waterways, producing offensive odor over time and lead to more environmental problems [18]. Zinc oxide nanoparticles and nanocomposites have been explored for the uptake of various pharmaceuticals as well as other pollutants, and results have shown that they are effective adsorbents for the sorption of pharmaceuticals [19,20,21]. Zinc oxide is non-toxic and easy to manufacture, and changes in environmental conditions do not affect its structure [22]. The wide band gap of 3.2 eV, an isoelectric point of 9.5, and large excitation binding energy of 60 MeV have made ZnO a nanoparticle of interest amongst researchers, thereby making the loading of ZnO nanoparticles onto base adsorbents an area of interest in recent years. Mohammed et al. [23] investigated the uptake of antibiotics using pistachio shell powder loaded with ZnO nanoparticles and results showed that loading ZnO onto the base material improved its adsorption efficiency by increasing the surface area,
Researchers have therefore found ways to improve the uptake capacity and efficiency of agro-waste adsorbents by surface modification in order to improve the surface area, porosity, pore size, and volume [24]. This can be carried out through carbonization (physical activation) and chemical activation (using acids, bases, or salts) [25].
The formation of nanocomposites with the activated carbon creates and incorporates unique features and higher surface area and produces adsorbents with higher uptake capacity. These composites have high reusability capacity and can be applied multiple times without losing their efficiency [26].
In this study, PPAC-ZnO nanocomposite was used in a batch system for the uptake of Chloroquine. The objective of this research is to monitor and study the effects of initial concentration, time, and temperature on the uptake capacity of PPAC-ZnO on chloroquine. The Langmuir, Freundlich, Temkin and Dubinin Radushkevich isotherms were used to monitor the uptake behavior and nature of the adsorption. Kinetic models (pseudo-first and second-order, Elovich, and intraparticle diffusion) were used to evaluate the experimental data. Furthermore, the thermodynamics of this process was studied.
2 Materials and methods
2.1 Reagents and apparatus
Analytical-grade reagents from Sigma-Aldrich, USA, and Fisher Scientific, Germany, were used throughout this study. Orthophosphoric acid (H3PO4) (BDH chemicals CAS:7664–38-2), ammonium carbonate (NH4CO3) (Sigma-Aldrich CAS:506–87-6), distilled water, chloroquine (Sigma-Aldrich CAS:747–36-4), (Chemical structure of chloroquine is presented in Fig. 1), sodium hydroxide (NaOH) (Carlo Erba CAS: 1310–73-2), pH meter (Hanna HI 2210), zinc nitrate (Zn(NO3)2 (LOBA Chemie CAS: 10196–18-16), magnetic stirrer (Bante MS300), crucible, desiccator, evaporating dish, sieve, oven (GENLAB N30C), furnace (Searchtech SX-5–12), and plantain peel (PP) were used in this study.
2.2 Material preparation/carbonization
Plantain peel was obtained from the Landmark University research farm. After collection, they were washed thoroughly with water, cut into smaller sizes, and then sundried for 3 days. They were then placed in an oven for further drying at 100 °C. It was then ground to fine powder allowed to carbonize in a furnace at temperature 400 °C for 1 h to form PP [27].
2.3 Chemical activation of plantain peel using H3PO4
Fifty grams of the PP was placed in a beaker and 1000 cm3 of 1.0 M orthophosphoric acid was added and mixed. The beaker was placed on a heating mantle and allowed to heat until a paste was formed. After cooling, the slurry was transferred to a crucible and heated in a furnace at 400 °C for 1 h. after which it was left to cool then washed severally until a neutral pH was attained. This was dried in an oven, transferred to an airtight container for storage and labelled as PPAC [28].
2.4 ZnO nanocomposite synthesis
The precipitation method described by Raoufi [29] with slight modification was used for the synthesis of ZnO nanocomposites. (NH4)2CO3 (1.5 M) with 5 g the activated carbon (PPAC) was stirred in a beaker on a magnetic stirrer and Zn (NO3)2 (1.0 M) was slowly introduced resulting in the formation of grey particles. The sample was filtered and the precipitate rinsed with ethanol and distilled water repeatedly. It was then transferred to a crucible and dried at 100 °C for 6 h. After which it was calcinated at 550 °C for 4 h. The resulting nanocomposite was labelled PPAC-ZnO-NC.
2.5 Physicochemical parameter determination
2.5.1 Determination of pH
One gram of the sample was placed in a beaker and 100-mL water was added to it. It was placed on a heating mantle and allowed to boil for 5 min. The content was left to cool and made up to the 200 mL mark with distilled water. The pH was then measured using a pH meter [30].
2.5.2 Moisture content determination
Moisture content was determined using the method as described by [31]. In triplicates, and 1.0 g of the adsorbent was weighed into a crucible then placed in an oven for about 5 h at 105 °C. It was then placed in a desiccator and left to cool before reweighing. The difference in weight between the initial and final mass was noted and the % moisture content was calculated using Eq. 1.
2.5.3 Determination of ash content
The % ash content was determined using the procedure as described by Dada et al. [28]. Measurement was done in triplicate. One gram of the sample was placed in crucibles and heated in a furnace at 500 °C for 1 h 30 min. After which, it was allowed to cool in a desiccator and then reweighed. Equation 2 was applied to calculate the ash content.
2.5.4 Volatile matter
To determine the amount of volatile matter, an adsorbent mass of 1.0 g was weighed into a crucible and allowed to heat for 10 min at a temperature of 500 °C [18]. Calculation was done using Eq. (3).
2.5.5 Determination of bulk density
A 10 cm3 measuring cylinder was weighed before and after packing with water. The same cylinder was then packed with the sample with constant tapping in order to ensure tight packing of the sample. After which it was weighed. [28].
The weight difference was noted and the bulk density was evaluated using Eq. 4:
where W1= weight of empty measuring cylinder; W2= weight of cylinder filled with sample, and V = volume of cylinder.
2.5.6 Simple specific surface area by Saer’s method
A total of 0.5 g of the sample was placed in a beaker and 0.1 M HCL was used to reduce its pH to 3–3.5 after which 10.0 g of NaCl was added. Deionized water was added to make up its volume to 50 cm3 and the content of the beaker was titrated with NaOH (0.1 M) to pH 4 and further to pH 9. The volume needed to raise the pH from 4 to 9 was recorded and the surface area was calculated using Eq. 5 [28]:
2.5.7 Point of zero-charge (PHpzc)
This value gives us the pH at which the charges on the adsorbent surface is null. The pHpzc was determined first by the addition of 0.1 g of activated carbon to NaCl (0.1 M) whose pH has been set from 2 to 12 using HCl or NaOH. The container was covered and allowed to shake for 24 h then the final pH was measured. The pHpzc is the point where there is no change in pH [30].
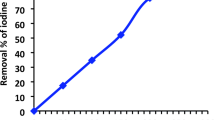
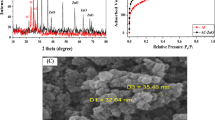
2.5.8 Iodine number and surface area calculation
For the determination of iodine number, the method is described in the literature [27]. A total of 0.5 g of the adsorbent was added to 100 mL standard iodine solution and 10 mL of 5% HCl in a 100-mL flask. The solution was kept on a shaker for 20 min after which it was filtered and about 20 mL of the filtrate was titrated with sodium thiosulphate (0.1 M) with starch serving as the indicator. The value obtained for titration of blank was also recorded. The % amount of iodine adsorbed was determined using Eqs. 6 and 7:
The iodine value was calculated using the formula as described in the literature [32].
where C1 and C2 (mol/L) are the concentrations of stock iodine solution and sodium thiosulfate respectively. M is the mass of adsorbent used, V2 (mL) is the volume of sodium thiosulphate used, and D is the correction coefficient.
The surface area calculated from the iodine number (SBET) was further calculated using the Eqs. 8 and 9 [33];
2.5.9 Boehm titration (determination of oxygen-containing functional groups)
The Boehm titration was used for the determination of the surface functionalities of the adsorbent. For the acidic group determination, 1 g of the sample was placed into a beaker containing 15 mL of NaOH (0.1 M), NaHCO3 (0.1 M), and Na2CO3 (0.05 M) based on the consideration that they neutralize carboxylic, lactonic, and phenolic groups. They were kept on a shaker for 48 h. After which it was back titrated with HCl (0.1 M). For the determination of basic groups, 0.1 M HCl was used and titrated with NaOH (0.1 M). The volume for titration was noted and the amount of oxygen-containing functional groups was calculated using Eqs. 10 and 11
where Vbx and Vex stand for the volume of titrant used to titrate the blank and samples respectively. Fx stands for the amount of oxygen-containing functional groups (mmolg−1), DF stands for the dilution factor, and Mt stands for the number of moles of the titrant.
2.6 Adsorption studies
For the adsorption studies of chloroquine using PPAC-ZnO nanocomposites, in a conical flask, 0.1 g of the nanocomposite was introduced into 100 mL of the adsorbate which was then subjected to shaking using a mechanical shaker. The adsorbent was then filtered and the concentration of the residue was obtained using a UV spectrophotometer. Equation 12 was used for the calculation of quantity adsorbed.
where Ce and Co represent the initial concentration (mg/L) and concentration at equilibrium (mg/L) respectively of adsorbate; V is the volume of the solution (L); m represents the mass of the adsorbent (mg); and Qe stands for the adsorption capacity (mg/g) of the adsorbent.
For the determination of the removal efficiency of the adsorbate, Eq. 13 was used.
where Co and Cf stand for the initial and final concentration (mg/L) of adsorbate after the adsorption process.
2.6.1 Adsorption parameters
The effect of time between the adsorbent and adsorbate was evaluated by monitoring the adsorption between 10 and 120 min at various time intervals. The absorbance and residual concentration were periodically monitored using a UV–Vis spectrophotometer. It was expedient to monitor the contact time because it affects the overall adsorption process, adsorption kinetics as well as the economic efficiency of the process [34]. The effect of temperature on the adsorption process was monitored by studying the uptake under temperatures 30, 40, and 50 °C. The effect of initial concentration was also monitored by varying concentrations from 10, 20, 30, 40, and 50 ppm and a working volume of 100 mL.
3 Results and discussion
3.1 Adsorbent characterization
3.1.1 Physicochemical characteristics
The pH and pHpzc were found to be at 7.02 and 4.98 respectively. Figure 2 shows the graph of pHpzc. This shows that at values above the pHpzc, the solution becomes negatively charged and favors the uptake of cationic species. As shown in Table 1, the low values of ash, moisture, bulk density, and volatile matter content reveal that the density of the adsorbent particles is small and as such a suitable adsorbent for use. This could largely be due to the activation and carbonization process that removes volatile components and dries the sample to a large extent. It has been reported that an ash value between 1 and 20% is suitable for the effective uptake of pollutants. The amount of oxygen-containing functional groups indicating the amount of acidic and basic sites were calculated as shown in Table 2. The total acidic sites were found to be 0.18 while the total basic sites were 1.13. Boehm titration gives a fan estimate of the surface functionalities of the adsorbent. It is assumed that HCl neutralizes basic groups while NaHCO3, NaCO3, and NaOH neutralizes acidic groups. The iodine value gives a rough estimate of the porosity of the adsorbent and can be used to estimate the surface area hence, giving us an idea of the adsorbent capacity. The high values obtained for iodine as shown in Table 3 show the presence of large micropores and large surface area obtained due to the activation and carbonization process. The iodine value can be used to estimate the surface area. Values obtained show that the surface of PPAC-ZnO-NC is large enough for chloroquine uptake.
3.1.2 Surface chemistry of PPAC-ZnO
The nature of the surface properties and functional groups present in the adsorbent were investigated using FTIR. As shown in Fig. 3, before adsorption, notable peaks were observed from the results at 2600–3000 cm−1 corresponding to and indicating the existence of the O–H group, 1000 cm−1, 1047 cm−1, and 963 cm−1 corresponding to C–O stretch and C–H stretch respectively. The O–H signal appeared to be of low intensity probably caused by the intense moisture loss as a result of calcination of the nanocomposite during its synthesis. Peaks at 963 cm−1 showed clearly the presence and formation of ZnO nanoparticles on the adsorbent. After the adsorption, however, OH bands of high intensity are observed at 3330 cm−1. The corresponding disappearance and appearance of new bands showed the chloroquine molecule reacted with the adsorbent surface.
XRD images of PPAC/ZnO nanocomposite as shown in Fig. 4 were carried out to establish the loading of ZnO nanocomposites onto the plantain peel activated carbon.
The SEM images of PPAC/ZnO nanocomposites before and after uptake of CQ are shown in Fig. 5A and B respectively. Before adsorption, surface morphology (Fig. 5A) showed the presence of pores, which serve as sites for adsorption and filling of pores were observed after adsorption of CQ (Fig. 5B) to indicate trapping of CQ molecules.
3.2 Effects of chloroquine solution temperature, initial concentration, and contact time
Five varying concentrations of 10, 20, 30, 40, and 50 ppm were used to investigate the adsorption process. The amount of chloroquine removed increased as agitation time increased at all initial concentrations of chloroquine. Similarly, the uptake of chloroquine increased as the initial concentration of chloroquine increased. Fast uptake was observed over the first 40 min and then slower uptake occurred until equilibrium was reached as shown in Fig. 6. The very fast rate of adsorption can be attributed to the presence of vacant sites for adsorption on the surface of the nanocomposite. However, the reduction in the adsorption rate can be attributed to electrostatic hindrance between chloroquine and the surface of the nanocomposite, leading to the unavailability of adsorption sites. Also, it can be observed that the time taken to reach equilibrium depended largely on the initial concentration as the lowest initial concentration reached equilibrium first. For this study, maximum adsorption removal was 78.88% at 10 ppm initial concentration at 323 K. The percentage removal efficiency increased because of the availability of more active sites until the adsorption sites were saturated at higher concentrations between 50 ppm. The increase in adsorption capacity with an increase in initial CQ concentration from 10 to 50 mg/L is a result of the increase in driving force due to the concentration gradient developed between the bulk of CQ solution and PPAC-ZnO surface. At higher CQ concentration, PPAC-ZnO active sites become saturated and pores filled up until equilibrium was reached at 120 min. A similar trend was observed by [35, 36].
3.3 Adsorption kinetic studies
Figure 7 shows the linear plot of pseudo-first-order (PFO), pseudo-second-order (PSO), Elovich, and intraparticle diffusion (IPD) kinetic model parameters for the adsorption of chloroquine. A better understanding of the rate of adsorption as well as the mechanism of the process was gotten from kinetic studies. From evaluated parameters presented in Table 4, disagreement between the calculated quantity adsorbed and experimental quantity adsorbed (qe, cal, and qe, exp respectively), lower values of R2 (R2 < 0.7) far away from unity, and higher values of SSE (112.286–699.661) and X2 (2.803–150.776) demonstrated that PFO is not suitable to describe the kinetics of adsorption of Chloroquine onto PPAC-ZnO. PSO best describes the kinetics of adsorption of CQ onto PPAC-ZnO. More so, a rapid increase of pseudo-second-order rate constant (min−1) as the concentration increases was observed indicating a rapid kinetic. From Table 5, qeexp and qecal were very close, and higher values of R2 > 0.97 coupled with lower values of SSE (0.236–0.066) and X2 (0.0282–0.00209) demonstrated the best fitting of the PSO model. This finding was supported by [13].
Figure 7C shows the plot of the Elovich model. The ∝ (initial adsorption rate, mg/g-min) and β (desorption constant, g/mg) were determined from the slope and intercept of the linear plot of qt versus ln (t). From this study, the initial chloroquine adsorption rate ( ∝) increases with an increase in concentration from 3.079 to 881.586 mg/g-min. However, since the R2 values were lower than 0.9, Elovich demonstrated a weak fit for the adsorption of chloroquine onto PPAC-ZnO.
The linear plot of IPD as observed in Fig. 7D shows the intraparticle diffusion model that participated in the adsorption process. This is evidence that chloroquine synthetic waste percolated into the pores of PPAC-ZnO. Studies have shown that if the plot of intraparticle diffusion did not pass through the origin, it is not the only rate-determining step [37, 38]. From this study, the IPD model is not the only rate-determining step since it does not pass through the origin. However, an increase in the intraparticle diffusion rate from 0.467 to 0.961 with an increase in initial CQ concentration demonstrated that the mechanism was pore dependent since a linear plot was obtained across the concentrations [39]. More so, the increase in boundary thickness from 2.211 to 21.217 as the concentration increases demonstrated that the surface sorption contributed to the rate-determining step. Dada et al. [40] from previous studies reported that the larger the intercept, the greater the contribution of the nano adsorbent in the adsorption process. A similar trend was observed in this study which is also supported by [41].
3.4 Adsorption isotherms
The adsorption isotherm models used to study the adsorption of chloroquine using PPAC-ZnO nanocomposites were the Langmuir, Freundlich, Temkin, and Dubinin Radushkevich isotherm models, and their plots are indicated in Fig. 8. The Langmuir model assumes that the nature of the adsorbate coverage on the surface of the adsorbent is homogenous. Based on the RL values, a value of (0 < RL < 1) shows that the adsorption is favorable while values of (RL > 1) show that the uptake is unfavorable. (RL = 1) shows that the uptake is linear and (RL = 0) shows that it is irreversible. As indicated in Table 6, all RL values were within the 0–1 range, thereby showing that the conditions were favorable for the uptake of chloroquine.
Freundlich however assumes that the nature of the adsorbate coverage on the adsorbent is heterogeneous with a non-uniform distribution of heat of adsorption. The KF and n values which represent the adsorption capacity and intensity are important parameters to be noted. For proper uptake of adsorbates, it is important that the KF and n values are within the range of 1–10. The increase in KF and n values as shown in Table 5 suggests that the uptake may be exothermic and favorable at all temperatures. The Temkin model assumes that as coverage on adsorbent occurs as a result of interactions, the heat of adsorption of all molecules in the layer decreases linearly. Also, this model assumes that adsorption is characterized by a uniform distribution of binding energies up to some maximum binding energy. The high KT values showed a strong interaction between chloroquine and adsorbent surface. The Dubinin-Radushkevich model assumes that the adsorption is multi-layer in nature and therefore indicates the physical adsorption process.
3.5 Adsorption thermodynamic studies
Thermodynamic studies were carried out to determine the nature, spontaneity, and feasibility of chloroquine uptake. The Gibbs free energy ΔG value can be used to determine whether the process is feasible and spontaneous or not. The thermodynamics plot is shown in Fig. 9. The enthalpy ΔH values are used to understand the nature of heat transfer, whether endothermic or exothermic while the entropy change ΔS describes the degree of disorderliness. As shown in Table 7, the negative ΔG values show that the uptake is spontaneous while the negative ΔH shows that the uptake is endothermic. The ΔS values show that the level of randomness increases at the interface between the solid and liquid and as such spontaneous and thermodynamically favored. The activation energy value was derived as 40 KJmol−1 which reveals that physisorption takes place. This Ea value corresponds to the E value (below 8 kJmol−1) obtained from the D-R plot.
4 Conclusion
Plantain peel–supported zinc oxide was effective for the sorption of chloroquine from an aqueous solution. From the analysis of the results obtained, it was found that a removal efficiency of 78.89% was possible with the PPAC-ZnO nanocomposite at a concentration of 10 ppm and 313 K temperature. The nature of the adsorbate-adsorbent interaction was homogenous as the isotherm model fitted both Langmuir and Temkin isotherms. The pseudo-second-order kinetics best describes this adsorption. The negative ◦G and negative H◦ values obtained using thermodynamic analysis revealed that the biosorption process of chloroquine by PPAC-ZnO was endothermic in nature favorable, and spontaneous. The E values indicate that physisorption is the type of adsorption that takes place. This present study revealed the efficiency of PPAC-ZnO nanocomposites in effective adsorption of chloroquine from aqueous solution.
References
Lindroos M, Hörnström D, Larsson G, Gustavsson M, Van Maris AJA (2019) Continuous removal of the model pharmaceutical chloroquine from water using melanin-covered Escherichia coli in a membrane bioreactor. J Hazard Mater 365(September 2018):74–80. https://doi.org/10.1016/j.jhazmat.2018.10.081
Babıć S, Dabıć D, Ćurkovıć L (2017) Fate of hydroxychloroquine in the aquatic environment. In: 15th International Conference on Environmental Science and Technology, Rhodes, CEST2017_00817, September 2017, p 1–5
Dabi D, Babi S, Skori I (2019) The role of photodegradation in the environmental fate of hydroxychloroquine. Chemosphere 230:268–277. https://doi.org/10.1016/j.chemosphere.2019.05.032
Abena PM, Decloedt EH, Bottieau E, Suleman F, Adejumo P, Sam-agudu NA (2020) Perspective piece chloroquine and hydroxychloroquine for the prevention or treatment of COVID-19 in Africa: caution for Inappropriate off-label use in healthcare settings. Am J Trop Med Hyg 102(6):1184–1188. https://doi.org/10.4269/ajtmh.20-0290
Marinho T et al (2021) Science of the total environment can use of hydroxychloroquine and azithromycin as a treatment of COVID-19 affect aquatic wildlife ? A study conducted with neotropical tadpole. Sci Total Environ 780:146553. https://doi.org/10.1016/j.scitotenv.2021.146553
Muhammed Y (2020) Biosafety and health molecular targets for COVID-19 drug development: enlightening Nigerians about the pandemic and future treatment. Biosaf Heal. https://doi.org/10.1016/j.bsheal.2020.07.002
Bensalah N, Midassi S, Ahmad MI, Bedoui A (2020) Degradation of hydroxychloroquine by electrochemical advanced oxidation processes. Chem Eng J 402(July):126279
Sun J, Wang J, Zhang R, Wei D, Long Q, Huang Y (2017) Chemosphere Comparison of different advanced treatment processes in removing endocrine disruption effects from municipal wastewater secondary ef fl uent. Chemosphere 168:1–9. https://doi.org/10.1016/j.chemosphere.2016.10.031
Ahmed MB, Zhou JL, Ngo HH, Johir AH, Sornalingam K (2017) Sorptive removal of phenolic endocrine disruptors by functionalized biochar : competitive interaction mechanism, removal efficacy and application in wastewater. Chem Eng J. https://doi.org/10.1016/j.cej.2017.11.041
Agboola OS, Bello OS (2020) Enhanced adsorption of ciprofloxacin from aqueous solutions using functionalized banana stalk. Biomass Convers Biorefinery. https://doi.org/10.1007/s13399-020-01038-9
Juela DM (2020) Comparison of the adsorption capacity of acetaminophen on sugarcane bagasse and corn cob by dynamic simulation. Sustainable Environm Res 30(23). https://doi.org/10.1186/s42834-020-00063-7
Balarak D, Bandani F, Shehu Z, Ahmed NJ (2020) Adsorption properties of thermally treated rice husk for removal of sulfamethazine antibiotic from pharmaceutical wastewater. J Pharmaceutical Res Internat’l 32(8):84–92. https://doi.org/10.9734/JPRI/2020/v32i830475
Mountassir E et al (2020) TiO 2 and activated carbon of Argania Spinosa tree nutshells composites for the adsorption photocatalysis removal of pharmaceuticals from aqueous. J Photochem Photobiol A Chem 388:112183. https://doi.org/10.1016/j.jphotochem.2019.112183
Inam EI, Etim UJ, Akpabio EG, Umoren SA (2016) Simultaneous adsorption of lead (II) and 3, 7- bis (dimethylamino)-phenothiazin-5-ium chloride from aqueous solution by activated carbon prepared from plantain peels. Desalination Water Treat:37–41. https://doi.org/10.1080/19443994.2015.1010236
Salman JM, Njoku VO, Hameed BH (2011) Adsorption of pesticides from aqueous solution onto banana stalk activated carbon. Chem Eng J 174(1):41–48. https://doi.org/10.1016/j.cej.2011.08.026
Adekola FA, Ayodele SB, Inyinbor AA (2018) Activated biochar prepared from plaintain peels: characterization and Rhodamine B adsorption data set. Chem Data Collect. https://doi.org/10.1016/j.cdc.2018.11.012
Agarry SE, Owabor CN, Ajani AO (2012) Modified plantain peel as cellulose- based low-cost adsorbent for the removal of 2, 6-dichlorophenol from aqueous solution: adsorption isotherms, kinetic modeling, and thermodynamic studies. Chem Eng Commun 200:8, 1121–1147, pp 37–41. https://doi.org/10.1080/00986445.2012.740534
Nworie FS, Nwabue F, Ikelle II, Ogah AO, Elom N, Illochi NO, Itumoh EJ, Oroke CE (2018) Activated plantain peel biochar as adsorbent for sorption of zinc(II) ions: equilibrium and kinetics studies. J Turkish Chem Soc A 5:1257–1270
Choina J et al (2015) The influence of the textural properties of ZnO nanoparticles on adsorption and photocatalytic remediation of water from pharmaceuticals. Catal Today 241:47–54. https://doi.org/10.1016/j.cattod.2014.05.014
Deb A, Kanmani M, Debnath A, Bhowmik KL, Saha B (2019) Ultrasonic assisted enhanced adsorption of methyl orange dye onto polyaniline impregnated zinc oxide nanoparticles: kinetic, isotherm and optimization of process parameters. Ultrason Sonochem 54(January):290–301. https://doi.org/10.1016/j.ultsonch.2019.01.028
Zhang F, Lan J, Yang Y, Wei T, Tan R, Song W (2013) Adsorption behavior and mechanism of methyl blue on zinc oxide nanoparticles. J Nanoparticle Res 15(11):1–10. https://doi.org/10.1007/s11051-013-2034-2
Sridhar R, Ramanane UU, Rajasimman M (2018) ZnO nanoparticles – synthesis, characterization and its application for phenol removal from synthetic and pharmaceutical industry wastewater. Environ Nanotechnol Monit Manag 10:388–393. https://doi.org/10.1016/j.enmm.2018.09.003
Mohammed AA, Al-Musawi TJ, Kareem SL, Zarrabi M, Al-Ma’abreh AM (2019) Simultaneous adsorption of tetracycline, amoxicillin, and ciprofloxacin by pistachio shell powder coated with zinc oxide nanoparticles. Arab J Chem 13(3):4629–4643. https://doi.org/10.1016/j.arabjc.2019.10.010
Alipanahpour E, Ghaedi M, Asfaram A, Mehrabi F (2019) Journal of industrial and engineering chemistry efficient adsorption of Azure B onto CNTs / Zn : ZnO @ Ni2P-NCs from aqueous solution in the presence of ultrasound wave based on multivariate optimization. J Ind Eng Chem 74:55–62. https://doi.org/10.1016/j.jiec.2018.12.050
Adegoke KA, Bello OS (2015) Dye sequestration using agricultural wastes as adsorbents. Water Resour Ind 12:8–24. https://doi.org/10.1016/j.wri.2015.09.002
Masoudian N, Rajabi M, Ghaedi M (2019) Titanium oxide nanoparticles loaded onto activated carbon prepared from bio-waste watermelon rind for the efficient ultrasonic-assisted adsorption of congo red and phenol red dyes from wastewaters. Polyhedron 173:114105. https://doi.org/10.1016/j.poly.2019.114105
Ekpete OA, Marcus AC, Osi V (2017) Preparation and characterization of activated carbon obtained from plantain (Musa paradisiaca) fruit stem. J Chem:1–6. https://doi.org/10.1155/2017/8635615
Dada AO, Ojediran JO, Olalekan AP (2013) Sorption of Pb2+ from aqueous solution unto modified rice husk: isotherms studies. Adv Phys Chem Article:1–6. https://doi.org/10.1155/2013/842425
Raou D (2013) Synthesis and microstructural properties of ZnO nanoparticles prepared by precipitation method. Renew Energy 50:932–937. https://doi.org/10.1016/j.renene.2012.08.076
Bello OS, Lasisi BM, Adigun OJ, Ephraim V (2017) Scavenging Rhodamine B dye using moringa oleifera seed pod. Chem Speciat Bioavailab 29(1):120–134. https://doi.org/10.1080/09542299.2017.1356694
Ekpete OA, Horsfall MJnr (2011) Preparation and characterization of activated carbon derived from fluted pumpkin stem waste (Telfairia occidentalis Hook F). Res J Chem Sci 1(3):10–16
Zheng J, Zhao Q, Ye Z (2014) Preparation and characterization of activated carbon fiber (ACF) from cotton woven waste. Appl Surf Sci 299:86–91. https://doi.org/10.1016/j.apsusc.2014.01.190
Abdullah AN, Abdullah SP, Amin MFM, Zainol AN (2018) Preparation and characterization of a new biocarbon material derived from Macaranga gigantea ( giant ‘ Mahang ’) leaf biomass as precursor. Mater Today Proc 5(10):21888–21896. https://doi.org/10.1016/j.matpr.2018.07.047
Sudhakar P, Soni H (2018) PT SC. Biochem Pharmacol. https://doi.org/10.1016/j.jece.2018.04.013
Nazal MK, Gijjapu DR, Abuzaid N (2021) Effective removal of methylated phenol and chlorinated phenol from aqueous solutions using a new activated carbon derived from Halodule uninervis waste. Colloid Interface Sci Commun 41(December 2020):100370. https://doi.org/10.1016/j.colcom.2021.100370
Fallou H, Cimetière N, Giraudet S, Wolbert D, Le Cloirec P (2016) Adsorption of pharmaceuticals onto activated carbon fiber cloths modeling and extrapolation of adsorption isotherms at very low concentrations. J Environmental Manag 166:544–555. https://doi.org/10.1016/j.jenvman.2015.10.056
Dada AO, Adekola FA, Odebunmi EO (2017) A novel zerovalent manganese for removal of copper ions : synthesis, characterization and adsorption studies. Appl. Water Sci. 7(3):1409–1427. https://doi.org/10.1007/s13201-015-0360-5
Bello OS, Chris T, Oluwakemi A, Alao C (2020) Sequestering a non - steroidal anti - inflammatory drug using modified orange peels. Appl Water Sci. https://doi.org/10.1007/s13201-020-01254-8
Inyinbor AA, Adekola FA, Olatunji GA (2016) Kinetics, isotherms and thermodynamic modeling of liquid phase adsorption of Rhodamine B dye onto Raphia hookerie fruit epicarp. Water Resour Ind 15:14–27. https://doi.org/10.1016/j.wri.2016.06.001
Dada AO et al (2020) Sustainable and low-cost Ocimum gratissimum for biosorption of indigo carmine dye: kinetics, isotherm, and thermodynamic studies. Int J Phytoremediation 0(0):1–14. https://doi.org/10.1080/15226514.2020.1785389
Yazidi A, Sellaoui L, Dotto GL, Bonilla-Petriciolet A, Fröhlich AC, Lamine AB (2019) Monolayer and multilayer adsorption of pharmaceuticals on activated carbon: application of advanced statistical physics models. J Mol Liq 283:276–286. https://doi.org/10.1016/j.molliq.2019.03.101
Acknowledgements
The authors acknowledge and appreciate the Management of Landmark University for the provision of research enabling environment for this study. Assistance received from staff and members of the nanotechnology laboratory is gratefully appreciated.
Author information
Authors and Affiliations
Corresponding authors
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Dada, A.O., Inyinbor, A.A., Bello, O.S. et al. Novel plantain peel activated carbon–supported zinc oxide nanocomposites (PPAC-ZnO-NC) for adsorption of chloroquine synthetic pharmaceutical used for COVID-19 treatment. Biomass Conv. Bioref. 13, 9181–9193 (2023). https://doi.org/10.1007/s13399-021-01828-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13399-021-01828-9