Introduction

A healthy environment is a necessity for the actualization and realization of Sustainable Development Goals (SDG). However, the global release of Endocrine Disruptive Chemicals (EDC) through unregulated anthropogenic activities is troublesome. This Endocrine Disruptive Chemicals (EDC) have been identified as emerging contaminants that can hamper the hormonal system at little doses leading to the following hazardous effects: cancerous tumors, birth defects, and developmental disorders1,2. EDC can cause hormonal dysfunction, deficit brain disorder, body deformation, breast, prostate, and thyroid cancers, many cases of sexual development problems. The hazardous effects of EDC are not alien to some of the negative effects of some dyes and antibiotics released into the environment. malachite green dyes3,4,5,6,7.

The cationic dye of interest in this study is Malachite Green (MG) because of its versatility. It has found application in leather industries and in aquaculture as antiparasitic. It is used as a coloring agent in wool, silk, paper, etc.8,9. However, MG has been reported to be toxic, carcinogenic, and mutagenic. Malachite green could cause damage to humans and animals through direct inhalation and ingestion contact leading to various negative effects such as carcinogenesis, mutagenesis, teratogenesis, respiratory toxicity, and reduced fertility10,11. Systems and sensory organs of the body have been reported to be adversely affected by malachite green dyes12,13. MG does not biodegrade easily; it is known to be resilient to fading on exposure to light and water. More so, its removal from contaminated water via common conventional techniques (biological and chemical precipitation) is tough. However, its affinity for dissociation in solution makes it prone to liquid–solid adsorption. A cleaner environment and sustainable cities as part of the sustainable development goals would be difficult to achieve if the problem arising from endocrine disruptive chemicals are not combatted. Some of the explored methods of wastewater treatment are advanced oxidation, adsorption, photocatalytic degradation, and biodegradation14,15. Exceptional among this treatment technique is adsorption owing to its ease of operation, low cost, adaptation to a broad range of dyes, and design flexibility16,17,18. Adsorption of pollutant using biomass such as agrowaste materials have attracted attention of researchers. Biomass-based adsorbents are sustainable materials derived among others from agricultural residues, forest, animal manures, food processing wastes and municipal wastes and they have found relevance in adsorption studies19,20. They are low cost, readily available and researchers have leveraged on their functionalization and modification potencials in order to increase their efficiency. Numerous biomass have been used in adsorption studies. Among agrowaste and biomass reported to be efficient are Sugarcane bagasse21, biomaterial & chelating agent (Chitosan)22, Palm oil shell activated biomass23,24. Several sorbents have been reported effective in uptake of this EDC dye (MG Dye): Ocimum gratissimum4, magnetic biochar25, Opuntia ficus-indica activated carbon26, almond gum9, Carica papaya wood27, MOF nanocomposites28 Silico-manganese fume (SMF) waste29 para-aminobenzoic acid modified activated carbon8. Strength of selectivity and increase in the capacity of the sorbent with high removal efficiency could be enhanced by biomass functionalization. This has necessitated our interest in the modification of our sustainable low-cost agro-residue, maize cob. As a result, in this study, orthophosphoric acid has been used to functionalized and modified maize cob as low-cost agro-waste with the focus of achieving better sequestration. In this study, Acid Functionalized Maize Cob (AFMC) was developed purposely to effectively biosorb malachite green cationic dye as a candidate of endocrine disruptive chemical. Mechanistic and isotherm modeling of biosorption were explored. The statistical validity of the models using different error models was also investigated. Pre-and-post-adsorption characterization by surface morphology using Scanning Electron Microscopy (SEM) and surface chemistry by FTIR.

Materials and methods

All chemicals used are of analytical grade. Orthophosphoric acid, H3PO4 (Loba Chemie), Hydrochloric acid, HCl (Loba Chemie CAS No: 7647-01-0, 37% purity), Sodium hydroxide, NaOH (Reckland Scientific Ec No: 215-185-5, 97% purity), Sodium Chloride, NaCl (Loba Chemie 99.5%, CAS: 7647-14-5), Malachite Green dye (CAS No.: 569-64-2; C23H25ClN2 (chloride); molar mass 364.911 g mol−1).

Acid Functionalized Maize Cob (AFMC) as low-cost adsorbent

Purposive and simple random sampling technique which is the best time saving technique was used for the collection of the maize cob agro-waste from the dumpsite of the University being an Agricultural-based University. Maize cobs obtained from Landmark University (Agro-based University) were screened and cleaned thereafter dried at 105 °C for 5 h in Gen lab oven, crushed, grounded, and screened to 106 µm. Acid activation was carried out following the procedure in our previous study30 and elsewhere in other literature31 using 0.5 M ortho-phosphoric acid (H3PO4). A detailed typical procedure for the preparation of Acid Functionalized Maize Cob (AFMC) was explicitly presented in the supplementary material (SI).

Physicochemical and spectroscopic characterization of AFMC

Determination of pH of AFMC

pH determination of AFMC was done by boiling 1 g AFMC in 100 mL distilled water for a period of 5 min. This was allowed to cool and its pH value was measured using an ATP-6 pH meter.

Determination of AFMC bulk density

Weight difference divided by the volume as depicted in Archimedes’ principle was used for bulk density determination as depicted in Eq. (1)32

$$Bulk\;density = \frac{{w_{2} - w_{1} }}{v}$$
(1)

W1 = Weight of empty measuring cylinder, W2 = combination of AFMC mass and the crucible, V = volume.

Determination of AFMC moisture content

Moisture content was determined typically by introducing 5 g AFMC into the initially weighed crucible and heated for 1 h at 105 °C. Evaluation of the moisture content was done using Eq. (2)42

$$\% \;Moisture\;content = \frac{{w_{2} - w_{3} }}{{w_{2} - w_{1} }} \times 100$$
(2)

W1 = Weight of crucible, W2 = Initial weight of crucible with sample, W3 = Final weight of crucible with sample.

Determination of AFMC surface area by Saer’s method

The AFMC surface area was determined using Sear's method. This involves acidifying 0.5 g of each adsorbent with 0.1 M HCl to a pH of 3–3.5. The volume was made up to 50 mL with distilled water after the addition of 1 g of NaCl. The titration was carried out with standard 0.1 M NaOH at 298 K to pH 4, and then to pH 9.0 following the procedure reported in the literature33,34. The volume needed to raise the pH from 4 to 9 was noted and surface area evaluated using Eq. (3):

$${\text{S}}\left( {{\text{m}}^{{2}} /{\text{g}}} \right) \, = {\text{ 32V}} - {25}$$
(3)

Batch biosorption studies

Preparation of malachite green adsorbate

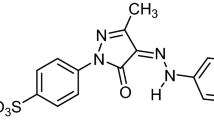
Analytical grade reagents were used all through the study. Stock solution of 1000 mg/L MG dye (Fig. 1) solution was prepared by dissolving 1 g MG salt in 1000 mL distilled water. A lower working concentration was prepared (100–600 mg/L) by serial dilution.

Figure 1
figure 1

Malachite Green dye structure.

Full size image

Biosorption operational parameters

Various Operational parameters relevant to this study were carried out following reported method3,4,35. The effect of pH was determined by varying the pH values between 3 and 10 via dropwise addition of 1 M HCl or NaOH where applicable. The effect of initial MG concentration was investigated by the introduction of 1 g AFMC into different concentrations of MG dye (100–600 mg/L). Variation of time as done to investigate the effect of contact time from 10 to 120 min. All through the study, the adsorbate-adsorbent system was agitated on the Orbital shaker to increase effective collision in the system. Measurement of residual concentration at maximum wavelength of 617 nm was done using double beam Libra Biochrom 5505 v1.0.4 PCB 1500 coupled with water Peltier system UV–Vis spectrophotometer.

Theory

Biosorption isotherm and kinetic modeling and statistical error validity

Equilibrium biosorption data obtained from the study of were analyzed using six of two-parameter models (Freundlich36, Langmuir16, Temkin37, Dubinni-Raduskevich38, Halsey39 and Jovanovic40). Similarly, both kinetics and mechanism models were fitted to Pseudo first-order41, Pseudo-second-order42, Elovich43, Fractional power44, Intraparticle45 and liquid film46 diffusion models. Estimation of the quantity adsorbed and percentage removal efficiency was done using Eqs. (4) and (5)47,48,49

$$Q_{e} = \frac{{\left( {c_{o} - c_{e} } \right)v}}{w}$$
(4)
$$\% RE = \frac{{c_{o} - c_{e} }}{{c_{o} }} \times 100$$
(5)

Presented in Tables 1 and 2 are the descriptions of both isotherm, kinetics, and mechanism models used in this study.

Table 1 Adsorption Isotherm Models (Non-linear and linear models with the description of parameters)46,47,48,49,50.
Full size table
Table 2 Kinetics and mechanism modeling of adsorption40,41,42,43,44,45,46,47,48,49,50,51.
Full size table

Adsorption statistical error function (ASRF) models

In most cases, determination of best fitting relationship and finalizing the best isotherm and kinetics model have always been through the use of linear correlation coefficient (R2) values. However. Owing to inherent bias from this transformation, the following four rigorous statistical error function models were used: Sum of square error (SSE)50; Hybrid fractional error function (HYBRID)39; Nonlinear chi-square test (χ2)51; Marquardt’s Percent Standard Deviation (MPSD)52, Presented in Table 2 are the equation of the Adsorption Statistical Error Function (ASRF) Models from Eqs. (24)–(27).

$${\text{Sum }}\;{\text{of }}\;{\text{Square }}\;{\text{Error}}\;{\text{SSE}} = \mathop \sum \limits_{i = 1}^{n} \left( {q_{e,cal} - q_{e,\exp } } \right)^{2}$$
(24)
$${\text{Non - linear - chi - square}}\;{\text{ test}}\;\chi^{2} = \mathop \sum \limits_{i = 1}^{n} \frac{{\left( {q_{e,cal} - q_{e,\exp } } \right)^{2} }}{{q_{e,cal} }}$$
(25)
$${\text{Hybrid}}\;{\text{ fractional }}\;{\text{error }}\;{\text{functions}}\;HYBRID = \sum\limits_{i = 1}^{n} {\left[ {\frac{{\left( {q_{e,\exp } - q_{e,cal} } \right)^{2} }}{{q_{e,\exp } }}} \right]}_{i}$$
(26)
$${\text{Marquardt's}}\;{\text{ Percent }}\;{\text{Standard }}\;{\text{Deviation}}\; \, \left( {MPSD} \right)MPSD = \mathop \sum \limits_{i = 1}^{n} \left[ {\frac{{\left( {q_{e,\exp } - q_{e,cal} } \right)}}{{q_{e,\exp } }}} \right]^{2}$$
(27)

Both isotherm and kinetics data were tested with the statistical error validity models.

Results and discussion

Physicochemical characterization

Figure 1 shows the structure of Malachite green as a cationic dye. Presented in Table S1 of the supplementary document is the physicochemical characteristics of Malachite Green (MG) indicating that it is a cationic dye having vast application. The unique physicochemical properties of AFMC were determined and summarized in Table S2. The pH determined was 6.75, surface area (1329 m2/g), 12% moisture content, 0.386 g/cm3 bulk density, and approximated particle size 300 μm < Ф < 250 μm. It has been reported that for applicability, activated carbon in the range of pH 6 to 8 is acceptable. The pH of AFMC determined as 6.75 is suitable for activated carbon (AC). The amount of water bound to activated carbon is determined via the moisture content. Lower moisture content is desirable for active activated carbon because of the competition of the water vapor with the pores of AC. The moisture content of AFMC lower than commercial activated carbon (CAC)53 is suitable. The filterability of activated carbon is determined from the bulk density.

Effect of pH

Shown in Fig. S1 is the effect of pH on biosorption of MG cationic dye onto AFMC. Ionic mobility and degree of ionization as well as the surface chemistry was influence by this operational parameter. Protonation, as well as ionic competition between H+ and MG+ zwitterion in aqueous solution for available sites, was observed between pH 2–5 at the acidic region. Higher quantity adsorbed and removal efficiency observed between pH 6 and 8 was due to deprotonation, low competition, and a higher aggregate of MG+. 7.425 mg/g quantity of MG was adsorbed at 100 ppm as observed at pH 6. Beyond pH 6, no further increase was observed, therefore pH 6 was chosen as an optimum pH similar to the finding of Alqadami et al. where MOF was used for adsorption of both Malachite green and methylene blue and optimum pH for highest adsorption capacity of MG was at 6.828.

Effect of initial concentration

Figure S2 of the supplementary document shows the result of the effect on initial concentration on effective removal of EDC cationic MG dye using AFMC. Lower transport of the MG dye at lower concentrations led to lower adsorption due to low driving force. However, the percentage of the percentage removal efficiency increased with increase in concentration. The concentration gradient developed was due to bombardment of the MG+ surrounding the active sites. It is obvious from Fig. S2 that rapid adsorption was observed at low concentration as a result of an increase in the active sites as compared to MG molecules in the bulk. Thereafter, diffusion, convection, and migration of MG molecules as a result of mass transport from the bulk lead to an increase in removal efficiency until a saturated point was reached. All the active sites were filled up at equilibrium and thereafter, no significant percentage removal efficiency observed. Similar finding was observed by Khan et al. and in the literature29,46,47.

Biosorption Isotherm modeling and statistical validity

Understanding of the binding interaction between AFMC and MG dye solution is enhanced by the study of the isotherm models. Equilibrium data were fitted to six isotherm models namely; Freundlich (Fig. 2A), Langmuir (Fig. 2B), Temkin (Fig. 2D), Dubinin-Raduskevich (Fig. 2E), Halsey (Fig. 2F), and Jovanovic (Fig. 2G). Portrayed in Fig. 2A–G are the isotherm models’ linear plots. Better fit with R2 > 0.97 were observed in Table 3a for Freundlich, Temkin, Dubinin–Raduskevich (D–R), Halsey. Equilibrium data did not fit well to Langmuir and Jovanovic considering their R2 value less than 0.92 (Table 3). Both Freundlich and Halsey isotherm models describe the adsorption characteristic for the heterogeneous surface. The characteristics parameters of Freundlich isotherm models are KF (adsorption capacity) and 1/nF and nF (adsorption intensity) obtained from the linear plot of log Qe against log Ce. The function of the strength of adsorption of MG onto AFMC is determined from the parameter 1/nF. The value of 1/nF (2.1372) being above unity is an indication of a cooperative adsorption54,55. The favourability of the adsorption process of MG onto AFMC could be affirmed from the Langmuir dimensionless and separation factor (RL). The RL value indicates the adsorption nature to either unfavorable or unfavorable. It is unfavourable if RL > 1, linear if RL = 1, favourable if 0 < RL < 1 and irreversible if RL = 0. The value of RL ranges between 0.00377 and 0.0744 and being less than one indicated favorable adsorption. There are many studies carried out on the adsorption of MG onto different adsorbents. Comparison of the Qmax monolayer capacities of adsorption of MG onto various adsorbents was presented in Table 4. Qmax of AFMC surpassed all those adsorbents compared indicating that AFMC is a better adsorbent for MG adsorption.

Figure 2
figure 2

(A–G) Plots of: (A) Freundlich isotherm model, (B) Langmuir isotherm model, (C) Separation Factor on sorption of MG onto AFMC, (D) Temkin isotherm model, (E) D–R isotherm model, (F) Halsey isotherm model, (G) Jovanovic isotherm model for sorption of MG dye onto AFMC.

Full size image
Table 3 Isotherm models’ parameters and for adsorption of malachite green onto AFMC.
Full size table
Table 4 Comparison of the Qmax monolayer capacity of MG adsorption with other adsorbents.
Full size table

The Dubinin–Kaganer–Raduskevich is generally applied to determine the mechanism of the MG-dye and AFMC system with a Gaussian energy distribution onto a heterogeneous surface. The R2 > 0.98 is an indication of a better description of equilibrium data by The DKR mean energy (E) value being less than 8 kJ indicated that the mechanism is physisorption. Studies from Bello et al. on scavenging of MG onto Citrus grandis peels further supported these findings38,56.

Statistical error validity on isotherm model

Studies have shown that the determination of the best isotherm model does not only depend on the R2 value. Statistical validity model has been introduced to further justify the suitability of the best isotherm model to describe the adsorption process49,59. Table 5 has shown the values of the experimental and calculated quantity adsorbed, Qe, exp and Qe, cal, respectively. The four most used statistical validity models in adsorption studies explored are SSE, HYBRID, X2, and MPSD. Adsorption Statistical Error Function (ASRF) has always been the most reliable validity parameter in justifying the best isotherm model for the equilibrium studies. To determine the isotherm best model, coupled with the higher R2 value, there must be closeness between the data of the Qe, cal, and Qe, exp alongside a low value of the ASRF60,61. Considering Table 5, Freundlich, Temkin, and Halsey isotherm models fit well into these conditions for fitness. From Table 4, the R2 values (0.9726 for Freundlich, 0.9726 for Halsey and 0.9846 for Temkin) are closer to unity with consistent agreement between Qe, exp and Qe, cal (254.13 mg/g and 293.43 mg/g for Freundlich; 254.13 mg/g and 243.75 mg/g for Temkin; 254.13 mg/g and 293.51 mg/g for Hasley).

Table 5 Adsorption statistical error function (ASRF) data on adsorption isotherm models.
Full size table

Effect of contact time at various initial concentrations

Importance relevant parameter that controls the transfer and build-up of charges from the bulk to the pore active site in all transfer media is the contact time. Effect of contact time was studied from 10 to 120 min at six different initial concentrations from 100 to 600 mg/L as depicted in Fig. S3 of the supplementary document. Based on the results, rapid adsorption was observed in the first 30 min dues increase attractive forces between the active sites and MG molecules as a result of van der Waals forces and electrostatic attractions. Between 60 and 90 min not significant increase in adsorption capacity and removal, efficiency was observed due to attainment of saturation and equilibrium. A fast diffusion onto the external surface of AFMC was followed by fast pore diffusion into the intraparticle matrix as a result of the participation of the functional groups until equilibrium was attained where 93.09% removal efficiency was achieved. The reaction was allowed to proceed till 90 min beyond which to increase was observed as depicted in Fig. 5. This finding is supported by the report of Hamdaoui et al.57 as well as Figen and Bayrak58.

Kinetics and mechanism model of MG sequestration

The rate of binding of MG onto AFMC was determined by the adsorption kinetics which also helps in gaining insight into the mechanism of the sorption process. Across various concentrations from 100 to 600 mg/L, the kinetic data were fitted to the following kinetics and mechanism models: Pseudo first-order (PFO)(Fig. 3A), Pseudo second-order (PSO) (Fig. 3B), Elovich (Fig. 3C), Fractional power (power function) (Fig. 3D); Intraparticle Diffusion (Fig. 3E) and Liquid film diffusion (Fig. 3F). Based on the evaluated data presented in Table 6, correlation coefficient R2 of pseudo-second-order (> 0.99) is highest among all the kinetics models explored. The R2 value is consistently higher and increases as the concentration increases. The h2 initial pseudo-second-order adsorption rate constant increases from 23.92 to 105.26 mg/g/min suggesting a rapid kinetic process. The error bars on the kinetic plots from Fig. 3A–D showed that the kinetic models were validated using statistical error functions. The consistency of the calculated adsorption capacity (Qe, cal) with the experimental adsorption capacity (Qe, exp) coupled with lower values of the statistical error function validity data as observed in SSE, HYBRID, X2, and MSPD further supported the PSO as the best kinetic model in this study. This result is supported by the investigation carried out by researchers59,60.

Figure 3
figure 3figure 3

(A) Pseudo first-order kinetics model (Conditions; pH 6, AFMC dose = 100 mg, contact time:90 min; concentrations: 100–600 mg/L). (B) Pseudo second-order kinetics model (Conditions; pH 6, AFMC dose = 100 mg, contact time:90 min; concentrations: 100–600 mg/L). (C) Elovich kinetics model (Conditions; pH 6, AFMC dose = 100 mg, contact time: 90 min; concentrations: 100–600 mg/L). (D) Fractional power kinetics model (Conditions; pH 6, AFMC dose = 100 mg, contact time:90 min; concentrations: 100 – 600 mg/L). (E) Intraparticle diffusion model (Conditions; pH 6, AFMC dose = 100 mg, contact time: 90 min; concentrations: 100–600 mg/L). (F) Liquid film diffusion mechanism model (Conditions; pH 6, AFMC dose = 100 mg, contact time: 90 min; concentrations: 100–600 mg/L). (G) Schematic diagram of the adsorption of MG dye onto AFMC (AFMC is depicted by its AFMC SEM morphology).

Full size image
Table 6 Parameters of kinetics models with associated Statistical Validity Data.
Full size table

Presented in Fig. 3D is the Fractional power plot for adsorption of MG onto AFMC. Considering Table 6, the parameters v and k being positive, greater than unity, and increase with the increase in concentration suggested a rapid kinetic process. The close agreement between Qe exp and Qe, cal are indications of the best fitting of the kinetic data to the fractional power model. At low concentration, the R2 values were far away from unity, however, better regression coefficients were obtained with higher concentration indicating the applicability of the adsorbent, AFMC, to the removal of pollutant at higher concentrations of MG dye. The choice of the best fit kinetic model was adjudged not only with correlation coefficient but also with the statistical error validity functions. It has been established that the model with a higher R2 value, nearness/closeness between Qe,exp and Qe, cal and lower data of statistical error function, would be chosen as the best descriptive model61,62,63,64. Pseudo second-order fit perfectly well into this condition and thus the best kinetic model to describe the sequestration of MG dye onto AFMC. Supporting this claim is the finding of Dehbi et al.65.

Figure 3E and F show the linear plots of Intraparticle Diffusion (IPD) and Liquid film diffusion (LFD) models. The evaluated parameters are presented in Table 7. Both the rate-controlling step and the diffusion mechanism were explored using IPD because its R2 values were consistently higher than that of the LFD. IPD would be the only rate-determining step if its plot begins from the origin. Contrary to this, the plot of qt against t1/2 did not begin from the origin hence IPD is not the only rate-determining step. However, the value of the thickness C of the adsorbent calculated from the IPD model being greater than zero across all concentrations indicated that the thickness of the boundary layer participated in the adsorption process. It is suggested that since boundary layer, C > 0 from the evaluated parameters in Table 7, another diffusion model may be involved in determining the rate-controlling step65.

Table 7 Mechanism model parameters of adsorption of MG onto AFMC.
Full size table

As reported by Dada et al.4,62 and Boparai et al.61, three definite steps involved in adsorption are: intraparticle or pore diffusion, where adsorbate molecules percolates into the interior of adsorbent particles; Liquid film or surface diffusion where the adsorbate is transported from the bulk solution to the external surface of adsorbent, and adsorption on the interior sites of the adsorbent. From this study, Pseudo second order (PSO) model best described the kinetic data as a result of a rapid adsorption process which is being supported by best R2 values and low statistical validity models. More so, the mechanism is pore diffusion dependent. Depicted in Fig. 3G is the scheme of mechanism of adsorption of malachite green onto AFMC. Adsorption is always a surface phenomenon. This scheme shows the summary of the adsorption of MG onto AFMC. Change in morphology was noticed after adsorption showing the evidence of the percolation of the MG dye into the pores and matrix of AFMC.

Surface morphology and surface chemistry post adsorption characterization

Evidence of the adsorption process was justified by morphological characterization of AFMC before and after adsorption onto MG using scanning electron microscopy (SEM). More so, surface chemistry was investigated by functional group determination using Fourier Transform Infrared (FTIR) spectroscopy. Before adsorption, dry and particle-like-crake nature with the presence of pores is evident all through the micrographs at different magnifications as portrayed in Fig. 4A,B. However, after adsorption as depicted in Fig. 4C,D, there was the disappearance of crakes, impregnated pores with MG dye solution, and robustness of AFMC adsorbent are morphology evidence of the adsorption process.

Figure 4
figure 4

(A, B) SEM morphology of AFMC before adsorption at 1000 μm and 2000 μm magnifications. (C, D): SEM morphology of AFMC after adsorption at 1000 μm and 2000 μm magnifications.

Full size image

Depicted in Fig. 5A,B are the FTIR spectra of AFMC before and after adsorption. The surface chemistry of AFMC before and after adsorption was investigated using FTIR. Broadband at 3390.70 cm−1 is attributed to O–H stretching of the hydrogen bonding which disappeared after adsorption as evidence of its participation in the adsorption process66. Aliphatic C–H stretching band at 2920.98 cm−1 was also found to decrease after adsorption. Carbonyl group, –C=O stretching vibration attributed to the lignin aromatic groups was assigned to 1714.28 cm−1 and 1667.29 cm−1. Ascribed to –C=C– bending of the Aromatic ring are the signals observed between 1515.10 and 1427.71 cm−1 while –CH3 bands as a result of deformation are observed at 1372.37 cm−1. Several bands between 1200 and 800 cm−1 are ascribed to characteristic carbohydrate bands while at 1049.93 cm−1, C–O vibrational band assigned to cellulose is observed at 1049.93 cm−1. The shift in bands and disappearance of functional groups confirmed their participation in the adsorption process67.

Figures 5
figure 5

(A) FTIR spectrum before adsorption of MG dye, (B) FTIR spectrum after adsorption of MG dye.

Full size image

Conclusion

This study has investigated the efficacy of Acid Functionalized Maize Cob (AFMC) as a sustainable, cost-effective, easy, unique, efficient adosrbent ultilizing adsorption as a low-cost technique for effective removal of malachite green (cationic dye). Unique physicochemical properties of AFMC vis-à-vis high surface area (1329 m2/g), moisture content (12%), bulk density (0.386) enhanced the adsorptive capacity. Adsorption of malachite green onto AFMC before and after was confirmed SEM and FTIR. Effective removal of malachite green was achieved at pH 6, 10–120 min contact time, six different initial concentrations from 100 to 600 mg/L concentrations at ambient temperature. A rapid and fast kinetics was attained at 90 min with 93%% removal efficiency. Based on higher R2 > 0.97 and lower suitable statistical validity models (SSE, HYBRID, X2, and MSPD), the equilibrium data were best described by Freundlich and Halsey isotherm models. The Langmuir adsorption mnolayer capacity (Qmax) of AFMC being 66.52 mg/g surpassed several adsorbents previously used for adsorption of MG. Free energy value being less than 8 kJ from DRK supported a physisorption mechanism. Based on R2 values and statistical error validity models, the kinetic and mechanism data were best fitted to Pseudo second order and supported by intraparticle diffusion. Subsequently, consideration could be given to AFMC as propitious material for environmental remediation.