Assessment of IRI and IRI‐Plas models over the African equatorial and low‐latitude region
Abstract
A reliable ionospheric specification by empirical models is important to mitigate the effects of the ionosphere on the operations of satellite‐based positioning and navigation systems. This study evaluates the capability of the International Reference Ionosphere (IRI) and IRI extended to the plasmasphere (IRI‐Plas) models in predicting the total electron content (TEC) over stations located in the southern hemisphere of the African equatorial and low‐latitude region. TEC derived from Global Positioning System (GPS) measurements were compared with TEC predicted by both the IRI‐Plas 2015 model and the three topside options of the IRI 2012 model (i.e., NeQuick (NeQ), IRI 2001 corrected factor (IRI‐01 Corr), and the IRI 2001(IRI‐01)). Generally, the diurnal and the seasonal structures of modeled TEC follow quite well with the observed TEC in all the stations, although with some upward and downward offsets observed during the daytime and nighttime. The prediction errors of both models exhibit latitudinal variation and these showed seasonal trends. The values generally decrease with increase in latitude. The TEC data‐model divergence of both models is most significant at stations in the equatorial region during the daytime and nighttime. Conversely, both models demonstrate most pronounced convergence during the nighttime at stations outside the equatorial region. The IRI‐Plas model, in general, performed better in months and seasons when the three options of the IRI model underestimate TEC. Factors such as the height limitation of the IRI model, the inaccurate predictions of the bottomside and topside electron density profiles were used to explain the data‐model discrepancies.
1 Introduction
Knowledge of the ionospheric variation is important to understand its effects on the operations of high‐frequency communications as well as space‐based positioning and navigation applications. Over the years, research efforts have been toward understanding the complexity and variability of the ionosphere, many of which have been documented. Several parameters have been used in these research efforts. Among these parameters, total electron content (TEC) is considered as the key parameter used in many ionospheric model applications [Bilitza and Reinisch, 2008]. GPS technology has made the estimation of TEC possible and thus provides a means of near‐real‐time ionospheric monitoring and hence has improved our understanding of the ionosphere.
For many years, the sparsity of GPS receivers has been a barrier to TEC investigation in the African region. The Africa region is located in the tropical region and has the largest tropical landmass in the world (https://www2.bc.edu). However, ionospheric effects on trans‐ionospheric signals have been reported to be more severe in tropical latitudes [Kintner et al., 2009]. Thus, the African region is located in an advantageous position for monitoring ionospheric dynamics. Ionospheric parameters derived from empirical models such as the International Reference Ionosphere (IRI) model, NeQuick, and many others, can serve as an alternative data set to specify the state of the ionosphere in regions like Africa that has limited number of continuous data sources. The performance of these models may largely depend on the techniques or the volume of ionospheric observations used in their development. Historically, the African region has remained under study due to fewer numbers of monitoring equipment. Consequently, discrepancies between the modeled and the observed ionospheric parameters are bound to exist in the region where there is no long‐term measurement for model development.
Among the empirical models, the IRI model has been recognized as the de facto standard for the climatological specification of ionospheric parameters such as electron density, electron temperature, TEC, and many more [Bilitza and Reinisch, 2008; Bilitza, 2009]. TEC is calculated in the IRI model by integrating through the entire ionospheric electron density profiles, i.e., the bottomside (region below the F2 peak) and topside (region above the F2 peak) electron density profiles. Although the bottomside portion contributes significantly to TEC, however, the main contribution comes from the topside portion. The need to improve the representation of the topside electron density profile has led to the development of several topside models [e.g., Bilitza, 1985; Rawer, 1990; Gulyaeva et al., 2002]. For the prediction of TEC, IRI model offers three options for the topside electron density model. They are the IRI 2001 (IRI‐01) option developed by Bilitza [2001], correction factor for the IRI‐2001 (IRI‐01 Corr) developed by Bilitza [2004], and the NeQuick option (NeQ) developed by Radicella and Leitinger [2001] and Coïsson et al. [2006].
The IRI model provides the monthly averages of ionospheric parameters in the altitude ranging from 60 to 2000 km [Bilitza et al., 2014]. In this case, the model may underestimate the true value of TEC since it does not account for electron contents between 2000 km and 20,200 km, which is the GPS orbital height. However, several models have been listed by the International Standardization Organization to extend the IRI model to plasmaspheric heights. The IRI Extended to Plasmasphere (IRI‐Plas) model is an acceptable international standard model for specifying ionospheric observables up to the plasmasphere region [Gulyaeva and Bilitza, 2012]. The plasmaspheric height limitation of IRI is overcome in the IRI‐Plas model; i.e., it provides a structural model of the ionosphere up to plasmasphere [Gulyaeva, 2010]. In IRI‐Plas model, the Russian Standard Model of the Ionosphere and Plasmasphere is combined with the IRI model [Chasovitin et al., 1998]. Both models used the International Radio Consultative Committee option for the prediction of the F2 layer peak parameters [Zakharenkova et al., 2015]. However, the IRI‐Plas model introduces scale height parameter to determine the shape of the IRI topside electron density profile [Maltseva et al., 2013]. Apart from the fact that the IRI‐Plas model specifies the ionosphere up to the plasmaspheric height, the model also has the advantage of integrating ionospheric dynamics into it for a better representation of the temporal variation in the ionosphere. This is achieved by ingestion of experimental values of TEC into the model [Gulyaeva, 2003].
In this present study, we evaluate the performance of the IRI 2012 and IRI‐Plas 2015 models over eight stations located in the southern hemisphere of the African region. To the best of our knowledge, this is the first time such validation of the IRI model and the latest version of the IRI‐Plas (IRI‐Plas 2015) in terms of TEC prediction is being done in the region simultaneously.
2 Data and Method of Analysis
In order to validate the two models over the region, TEC derived from GPS observations are compared to TEC predicted by the IRI‐Plas 2015 and the three topside options of the IRI 2012 models. The GPS data used are from eight GPS receivers stationed at different locations in the southern hemisphere of the African region as shown in Figure 1. Table 1 shows the geographic and geomagnetic coordinates of the locations of the stations used. The GPS data used for the study were recorded in the year 2014.
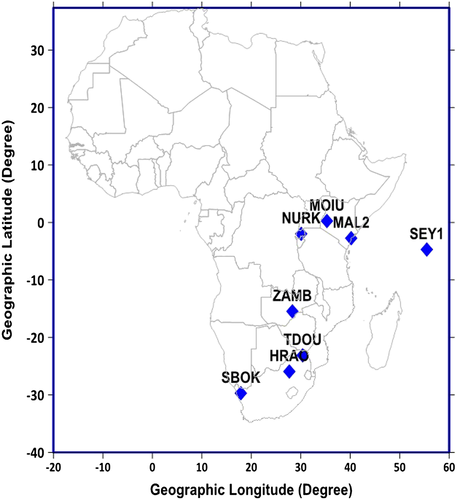
| Geographic Geomagnetic | |||||||
|---|---|---|---|---|---|---|---|
| Station | Country | Station's ID | Lat | Long | Lat | Long | Time (LT) |
| ELDORET | Kenya | MOIU | 0.29 | 35.29 | −2.69 | 107.64 | UT + 2 |
| KIGALI | Rwanda | NURK | −1.94 | 30.09 | −4.02 | 102.1 | UT + 2 |
| MALINDI | Kenya | MAL2 | −2.70 | 40.19 | −6.41 | 111.92 | UT + 3 |
| LA MISERE | Seychelles | SEY1 | −4.67 | 55.48 | −10.61 | 126.89 | UT + 4 |
| LUSAKA | Zambia | ZAMB | −15.43 | 28.31 | −16.93 | 97.96 | UT + 2 |
| THOHOYANDOU | South Africa | TDOU | −23.08 | 30.38 | −24.77 | 98.67 | UT + 2 |
| KRUGERSDROP | South Africa | HRAO | −25.89 | 27.69 | −27.07 | 95.42 | UT + 2 |
| SPRINGBOK | South Africa | SBOK | −29.67 | 17.88 | −29.11 | 84.19 | UT + 1 |
The estimation of TEC using the GPS technology is made possible because ionosphere introduces a frequency‐dependent delay on radio signals that propagate through it. The total number of electrons encountered by the signal along the satellite receiver path, known as the slant TEC (TECs) can be estimated from the combination of carrier phase and pseudorange of the GPS measurement. TECs, which is a function of the elevation angle of the satellite, passes and the spacing of the satellites in orbit may, however, pose a number of challenges due to spatiotemporal electron density gradient. To overcome this, the TECs is verticalized (converted to TEC that is independent of the satellite geometry) by dividing it by a factor, known as the obliquity or slant factor after the satellite and receiver biases have been removed, given by the expression in equation 1
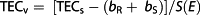 (1)
(1)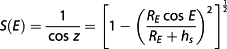 (2)
(2)The corresponding values of TEC from IRI 2012 and IRI‐Plas models were also computed for the same period. The three available topside options (NeQuick (NeQ), IRI 2001 corrected (IRI‐01 Corr), and IRI 2001 (IRI‐01)) of the IRI 2012 model were used. The online version of the model available at the National Space Science Data Center (NSSDC) website: (http://modelweb.gsfc.nasa.gov/ionos/iri.html) was used. Just like the IRI model, the IRI‐Plas also provides the monthly average value of ionospheric parameters. In this study, the recently released version of the IRI‐Plas model (i.e., IRI‐Plas 2015) was used to compute TEC. The latest version, which was implemented by the IONOLAB group, can be accessed through the online database of the Hacettepe University, Ankara, Turkey (www.ionolab.org). To provide the same level playing ground for both models, the “no extra input option” of the IRI‐Plas model was used to compute TECv, since the IRI‐Plas model has the option of incorporating GPS‐TEC whereas the IRI model does not.
For seasonal evaluation of the models, the months of the year were divided into four to represent the seasons. They are the March equinox (February, March, and April), June Solstice (May, June, and July), September equinox (August, September, and October), and December solstice (November, December, and January). The mean seasonal values of TEC were obtained by averaging the diurnal monthly mean values of TEC of the months in each division. To quantify the prediction error or the deviation of modeled values from the observed values, we calculated the root‐mean‐square deviation (RMSD) using the expression in equation 3.
 (3)
(3)3 Results
3.1 Diurnal Performance of the Models
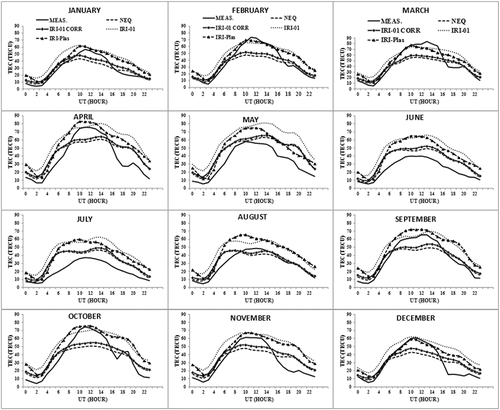
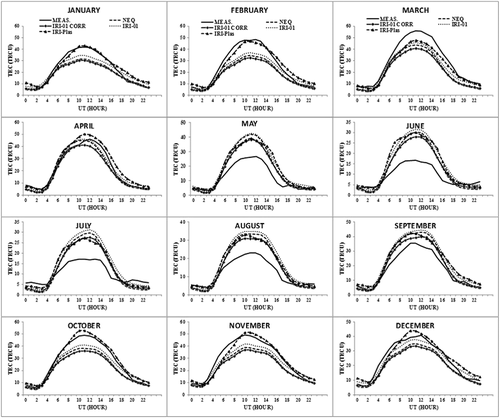
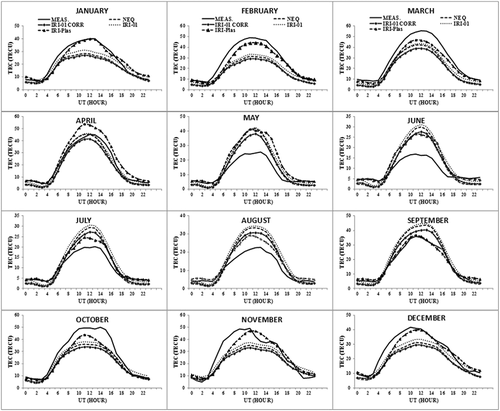
Figures 2-5 show the averaged diurnal monthly variations of the observed and modeled TEC at two stations located within the equatorial region (MOIU and MAL2) and two outside the region (HRAO and SBOK). The result obtained shows that both models reproduced the morphology of TEC quite well in the region, although with some upward and downward offsets. Generally, both models overestimate and underestimate TEC during the daytime and the nighttime. The two models overestimate TEC during the daytime in the months of May to September in all the stations and sometimes extend to the nighttime especially for stations within the equatorial region. The IRI model, in particular, the NeQ and the IRI‐01 Corr options, generally underestimate TEC in the remaining months during the daytime. In most cases, the IRI‐Plas performed better than the IRI model when the three options of the IRI model underestimate TEC during the daytime in most of the stations, especially in the months of February and March as shown in the diurnal variation plots in Figures 2-5 and the RMSD values in Table 2.

| Station | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MOIU | IRI‐NeQ | 6.86 | 12.32 | 14.37 | 13.24 | 13.42 | 10.90 | 11.85 | 5.93 | 8.83 | 11.88 | 10.24 | 10.64 |
| IRI‐01 Corr | 6.01 | 10.34 | 12.78 | 12.89 | 14.02 | 12.29 | 13.00 | 6.05 | 7.68 | 10.81 | 10.18 | 9.73 | |
| IRI‐01 | 14.10 | 12.61 | 14.51 | 22.13 | 26.54 | 23.68 | 23.58 | 14.78 | 13.84 | 16.99 | 19.57 | 16.15 | |
| IRI‐Plas | 10.24 | 9.99 | 10.24 | 16.96 | 15.75 | 19.58 | 19.51 | 14.95 | 13.23 | 15.45 | 16.44 | 11.30 | |
| NURK | IRI‐NeQ | 7.31 | 18.05 | 13.72 | 10.48 | 13.91 | 13.13 | 12.52 | 7.09 | 8.85 | 10.30 | 6.91 | 8.49 |
| IRI‐01 Corr | 7.41 | 15.24 | 11.84 | 9.59 | 15.12 | 14.88 | 14.08 | 7.81 | 9.30 | 9.08 | 7.28 | 6.59 | |
| IRI‐01 | 15.90 | 10.31 | 11.30 | 14.99 | 26.73 | 25.15 | 23.71 | 16.10 | 18.02 | 15.00 | 17.73 | 12.98 | |
| IRI‐Plas | 14.02 | 6.85 | 8.29 | 11.27 | 12.61 | 19.37 | 17.16 | 15.40 | 17.87 | 15.35 | 16.40 | 8.04 | |
| MAL2 | IRI‐NeQ | 6.66 | 15.60 | 13.70 | 8.70 | 16.87 | 15.39 | 14.59 | 6.61 | 7.06 | 9.08 | 7.35 | 7.90 |
| IRI‐01 Corr | 4.93 | 13.42 | 12.00 | 8.43 | 17.46 | 16.44 | 15.42 | 6.87 | 6.95 | 8.20 | 8.65 | 6.49 | |
| IRI‐01 | 10.93 | 8.85 | 9.95 | 16.27 | 28.84 | 26.34 | 24.66 | 13.93 | 13.83 | 13.94 | 19.28 | 12.04 | |
| IRI‐Plas | 8.98 | 5.35 | 6.63 | 10.71 | 14.19 | 19.01 | 16.33 | 10.99 | 11.82 | 12.97 | 16.40 | 5.92 | |
| SEY1 | IRI‐NeQ | 5.36 | 14.88 | 16.68 | 9.54 | 17.30 | 15.14 | 15.40 | 7.24 | 8.56 | 11.84 | 7.84 | 7.80 |
| IRI‐01 Corr | 4.63 | 13.90 | 16.31 | 9.56 | 16.34 | 15.08 | 15.25 | 7.44 | 8.41 | 11.23 | 8.32 | 6.53 | |
| IRI‐01 | 9.67 | 8.46 | 10.35 | 13.17 | 25.31 | 23.33 | 23.20 | 13.64 | 10.69 | 10.17 | 16.15 | 8.73 | |
| IRI‐Plas | 9.06 | 6.42 | 11.14 | 9.25 | 9.79 | 15.48 | 14.74 | 9.99 | 8.77 | 10.03 | 13.83 | 4.99 | |
| ZAMB | IRI‐NeQ | 4.93 | 5.94 | 6.12 | 5.39 | 11.20 | 7.92 | 8.34 | 9.54 | 6.39 | 4.96 | 3.45 | 3.47 |
| IRI‐01 Corr | 4.68 | 5.83 | 6.24 | 5.04 | 10.67 | 8.01 | 8.41 | 9.61 | 6.22 | 4.95 | 3.68 | 2.95 | |
| IRI‐01 | 6.47 | 4.18 | 5.72 | 10.15 | 15.79 | 12.21 | 12.56 | 14.40 | 11.45 | 6.12 | 7.36 | 5.72 | |
| IRI‐Plas | 6.52 | 4.06 | 4.23 | 7.18 | 8.48 | 8.54 | 7.27 | 9.05 | 7.42 | 5.06 | 6.42 | 5.01 | |
| TDOU | IRI‐NeQ | 5.13 | 9.30 | 6.89 | 4.29 | 8.66 | 8.25 | 4.91 | 6.80 | 5.46 | 5.87 | ‐ | 4.46 |
| IRI‐01 Corr | 5.58 | 10.11 | 8.05 | 2.74 | 7.04 | 7.50 | 4.03 | 5.60 | 3.92 | 6.94 | ‐ | 4.78 | |
| IRI‐01 | 3.00 | 6.69 | 4.71 | 5.46 | 10.03 | 10.04 | 6.21 | 8.51 | 7.36 | 4.20 | ‐ | 1.89 | |
| IRI‐Plas | 3.07 | 2.64 | 3.59 | 7.15 | 7.47 | 8.68 | 3.45 | 5.39 | 5.69 | 3.06 | ‐ | 3.25 | |
| HRAO | IRI‐NeQ | 5.99 | 8.50 | 8.72 | 2.96 | 8.11 | 7.07 | 6.51 | 6.82 | 5.61 | 6.27 | 6.94 | 4.58 |
| IRI‐01 Corr | 6.71 | 9.52 | 10.07 | 3.53 | 6.45 | 6.20 | 5.58 | 5.54 | 3.84 | 7.45 | 7.99 | 5.18 | |
| IRI‐01 | 4.45 | 6.80 | 6.77 | 2.43 | 9.13 | 8.38 | 7.56 | 8.09 | 6.87 | 4.47 | 4.85 | 2.56 | |
| IRI‐Plas | 3.38 | 3.54 | 5.43 | 3.81 | 8.31 | 8.14 | 5.71 | 6.38 | 5.88 | 2.46 | 3.53 | 3.61 | |
| SBOK | IRI‐NeQ | 6.80 | 0.53 | 9.68 | 3.38 | 7.84 | 6.42 | 4.52 | 6.34 | 5.39 | 8.66 | 8.56 | 7.09 |
| IRI‐01 Corr | 7.52 | 0.56 | 11.01 | 3.77 | 6.16 | 5.52 | 3.58 | 5.05 | 3.57 | 9.86 | 9.61 | 7.78 | |
| IRI‐01 | 5.11 | 0.46 | 7.95 | 2.12 | 8.32 | 7.32 | 5.31 | 7.26 | 6.03 | 7.13 | 7.47 | 5.15 | |
| IRI‐Plas | 3.00 | 0.35 | 5.61 | 5.28 | 9.40 | 5.62 | 2.43 | 3.94 | 1.54 | 6.48 | 6.19 | 3.75 | |
- a The numbers in bold indicate the value of the model with the lowest prediction error.
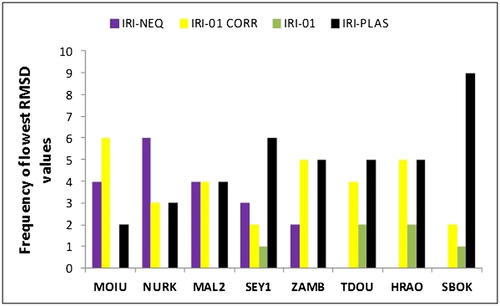
The bar chart in Figure 6 shows the frequency of the lowest RMSD values of the IRI‐Plas model and the three topside options of the IRI model in all the months in each station. Considering the individual options of IRI model, the NeQ and IRI‐01 Corr options performed better at stations close to the equator (MOIU and NURK), the IRI‐01 Corr option and IRI‐Plas model performed equally in MAL2, ZAMB, and HRAO, while the IRI‐Plas performed better in the remaining three stations (SEY1, TDOU, and SBOK) as shown also in Figure 2-5. In general, considering the options of the IRI model as a whole, the IRI model performed better than the IRI‐Plas model in most of the stations except in SBOK where the IRI‐Plas model performed better than the IRI model.
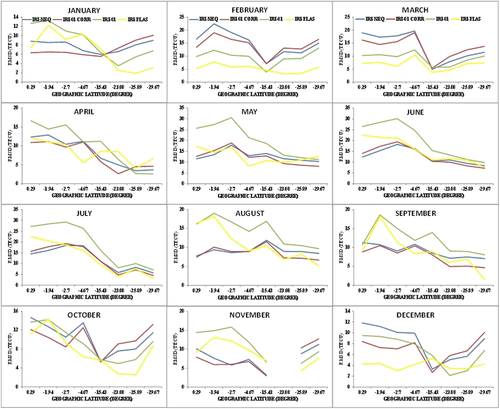
Figures 7 and 8 show the latitudinal distributions of RMSD values (i.e., prediction errors) for the two models for the daytime (06:00–17:00 LT) and nighttime (18:00–05:00 LT), respectively. The result shows that the prediction errors of both models exhibit latitudinal variation during the daytime and the nighttime; i.e., the prediction errors generally decrease with increase in latitude. Generally, the TEC data‐model divergence is most significant during the daytime and the nighttime at stations in the equatorial region. On the other hand, both models demonstrate most pronounced convergence during the nighttime at stations outside the equatorial region in most of the months. The RMSD values are highest at stations located within the equatorial region (up to 22, 19, 30, and 22 TECU during the daytime and 16, 16, 28, and 22 TECU during the nighttime for NeQ, IRI‐01 Corr, IRI‐01, and IRI‐Plas, respectively) and lowest at stations outside the region (as low as 3, 3, 2, and 1 TECU during the daytime and 2, 1, 1, and 1 TECU during the nighttime for NeQ, IRI‐01 Corr, IRI‐01, and IRI‐Plas, respectively). Also, the values of the prediction error of both models have the tendency to converge outside the equatorial region during the daytime in the months of May to July and in most of the months (except February and March) during the nighttime.
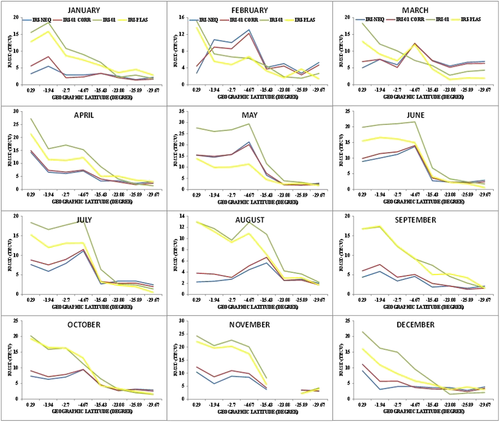
3.2 Seasonal Performances of the Models
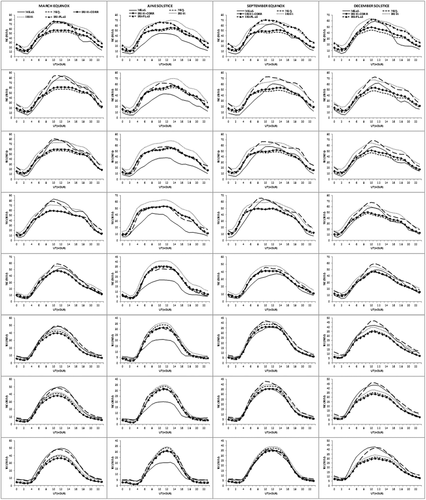
Figure 9 shows the seasonal averaged plots of the observed TEC and modeled TEC in all the stations. Generally, the modeled TEC are observed to follow fairly well with the measured TEC. However, significant discrepancies between the modeled and GPS‐TEC are observed and these showed seasonal trend. In March Equinox (MEQU), the IRI model, particularly the NeQ and IRI‐01 Corr options, generally underestimate TEC during the daytime in most of the stations (up to 28 and 24 TECU within the equatorial region and 11 and 14 TECU, respectively, for NeQ and IRI‐01 Corr options at stations outside the region). The TEC underestimation during this period appears to be less significant at ZAMB; a station located near the equatorial anomaly region. On the whole, the IRI‐Plas model performed better than the IRI model in most of the station as shown in Table 3.
| Station | MEQU | JSOL | SEQU | DSOL | |
|---|---|---|---|---|---|
| MOIU | IRI‐NeQ | 12.08 | 11.69 | 8.19 | 8.85 |
| IRI‐01 Corr | 10.87 | 12.82 | 7.46 | 8.30 | |
| IRI‐01 | 15.99 | 24.42 | 14.79 | 16.40 | |
| IRI‐Plas | 11.76 | 18.15 | 14.05 | 12.40 | |
| NURK | IRI‐NeQ | 13.30 | 12.66 | 7.84 | 7.15 |
| IRI‐01 Corr | 11.32 | 14.27 | 8.00 | 6.62 | |
| IRI‐01 | 11.10 | 24.94 | 16.11 | 15.40 | |
| IRI‐Plas | 8.08 | 16.21 | 16.00 | 12.61 | |
| MAL2 | IRI‐NeQ | 11.20 | 15.30 | 6.83 | 5.89 |
| IRI‐01 Corr | 9.71 | 16.17 | 6.71 | 5.42 | |
| IRI‐01 | 10.34 | 26.42 | 13.58 | 13.78 | |
| IRI‐Plas | 6.43 | 16.30 | 11.59 | 10.05 | |
| SEY1 | IRI‐NeQ | 12.21 | 15.35 | 7.66 | 5.83 |
| IRI‐01 Corr | 11.88 | 15.01 | 7.63 | 5.41 | |
| IRI‐01 | 8.58 | 23.56 | 10.67 | 11.18 | |
| IRI‐Plas | 7.27 | 12.99 | 8.74 | 8.48 | |
| ZAMB | IRI‐NeQ | 3.53 | 9.06 | 4.70 | 3.45 |
| IRI‐01 Corr | 3.75 | 8.95 | 4.82 | 3.26 | |
| IRI‐01 | 5.75 | 13.46 | 10.08 | 6.20 | |
| IRI‐Plas | 4.45 | 8.07 | 6.89 | 5.73 | |
| TDOU | IRI‐NeQ | 4.51 | 7.14 | 2.47 | 4.59 |
| IRI‐01 Corr | 5.54 | 6.06 | 1.31 | 5.00 | |
| IRI‐01 | 2.20 | 8.70 | 4.50 | 2.04 | |
| IRI‐Plas | 1.64 | 6.40 | 4.32 | 3.06 | |
| HRAO | IRI‐NeQ | 6.02 | 7.16 | 2.37 | 5.66 |
| IRI‐01 Corr | 7.35 | 6.01 | 0.98 | 6.47 | |
| IRI‐01 | 4.30 | 8.31 | 3.63 | 3.66 | |
| IRI‐Plas | 2.06 | 7.31 | 4.62 | 3.21 | |
| SBOK | IRI‐NeQ | 7.65 | 6.22 | 1.99 | 7.21 |
| IRI‐01 Corr | 8.85 | 5.06 | 1.47 | 8.07 | |
| IRI‐01 | 5.94 | 6.97 | 2.27 | 5.60 | |
| IRI‐Plas | 2.02 | 5.79 | 1.47 | 4.11 | |
- a The numbers in bold indicate the value of the model with the lowest prediction error.
In September Equinox (SEQU), TEC predicted by both models agree fairly well with the observed TEC for all hours at stations located outside the equatorial region (i.e., TDOU, HRAO, and SBOK). However, the IRI‐Plas model and the IRI‐01 option of the IRI models overestimate TEC for the whole day at stations located within equatorial region, with values up to 26 and 25 TECU for IRI‐01 and IRI‐Plas, respectively. The NeQ and IRI‐01 Corr options only overestimate TEC during the buildup period (i.e., between 04:00 and 09:00 UT) and underestimated TEC between the hours of 09:00 and 15:00 UT. Also, from Table 3, the lowest values of the prediction errors are generally observed at stations outside the equatorial region particularly during the SEQU. Overall, the IRI model, particularly the IRI‐01 Corr option, gives the best TEC prediction during the SEQU in most of the stations as shown by the bolded values of RMSD in Table 3.
In June Solstice (JSOL), both models generally overestimate TEC in all the stations (with values up to 24, 23, 35, and 26 TECU within the equatorial region and 14, 11, 15, and 12 TECU at stations outside the region for NeQ, IRI‐01 Corr, IRI‐01, and IRI‐Plas, respectively). However, the overestimation of TEC is observed for the whole day at stations within the equatorial region (MOIU, NURK, MAL2, SEY1, and ZAMB), while it is observed between 04:00 and 18:00 UT at stations outside the equatorial region. In general, the IRI model performed better than the IRI‐Plas in JSOL: the NeQ option performed better in most equatorial stations (except SEY1 and ZAMB where the IRI‐Plas performed better) while the IRI‐01 Corr performed better in the remaining stations, i.e., at stations outside the equatorial region. Also, from Table 3, the highest values of the prediction error of the two models are observed in JSOL particularly at stations in the equatorial region.
In December Solstice (DSOL), TEC predicted by the IRI‐Plas model and IRI‐01 option of the IRI model generally overestimated TEC for the whole day in stations within the equatorial region. The NeQ and IRI‐01 Corr options underestimate TEC between 09:00 and 14:00 UT and overestimated during the nighttime, particularly around the postsunset period at the equatorial stations. On the other hand, at stations outside the equatorial region, all the three options of the IRI model generally underestimate TEC in most hours, particularly during the daytime. On the whole, the IRI model (i.e., IRI‐01 Corr) gives a better description of TEC than the IRI‐Plas at stations in the equatorial region, while the IRI‐Plas model performed much better than the IRI model at stations outside the equatorial region.
4 Discussion
We examined the performances of the IRI and IRI‐Plas models in predicting TEC over the Southern African equatorial and low‐latitude stations. Some agreements as well as discrepancies between the measured and modeled TEC were observed. Discrepancy between the observed TEC and TEC predicted by the IRI model has been partly attributed to the height limitation of the model by several authors [e.g., Coisson et al., 2008; Venkatesh et al., 2011; Adebiyi et al., 2014, 2016; Satya Srinivas et al., 2013]. The IRI model estimates TEC by integrating the electron density profile between the path length of 60 and 2000 km, whereas the GPS derived TEC accounts for electron content up to the GPS orbital height (20,200 km). Since the IRI‐Plas model accounts for electron content up to the plasmaspheric altitude, therefore, the values of TEC predicted using the IRI‐Plas model are expected to be higher than the IRI model predictions. We observed from the diurnal monthly and seasonal plots of TEC values that all the options of the IRI model generally underestimate TEC in some periods in most of the stations, particularly in the months of February, March and during the MEQU, and also at stations outside the equatorial region in the DSOL. This corresponds to the period when the IRI‐Plas model performed better than the three options of the IRI model. This may suggest that the underestimation of TEC by the IRI model observed in the diurnal monthly and seasonal variation plots may be attributed to the failure of the IRI model to account for electron beyond the 2000 km height. Also, apart from the inclusion of the plasmaspheric contribution to TEC in the IRI‐Plas model, the offset between the IRI and IRI‐Plas models may also be due to the topside estimates in the two models. In the IRI‐Plas model, the topside basis scale height parameter was introduced to determine the shape of the topside profile [Maltseva et al., 2013]. We observed in some months that the IRI Plas predictions are lower than the IRI model. This may be due to the different approaches employed in the topside modeling between the two models.
Also, overestimation of TEC by both models was observed in some hours, particularly during the daytime, in the diurnal and seasonal variation plots. This may be attributed to the inaccurate prediction of the electron density profiles in the two models over the region. Electron density profile is a key parameter for modeling the ionosphere. TEC is calculated in both models by integrating the electron density profile from the D layer in the bottomside to the topside regions. In the IRI model, the bottomside electron density is modeled as a function of height and is described in terms of the thickness and the shape parameters. The bottomside region contributes 15%–40% of electron content to GPS‐TEC [Bilitza et al., 2012]. For the description of the thickness and shape parameters, the IRI model uses data from global ionosonde networks consisting mainly of data from the midlatitudes and other regions different from the African region. Unfortunately, since the African region is not well covered by ionosonde, this may contribute significantly to a less reliable IRI modeled‐thickness parameter in the region and with a consequent effect in the modeled TEC. On the other hand, the topside profile contributes the largest values to TEC and it is of great importance. It also serves as a foot point for plasmaspheric models [Gallagher et al., 2000; Gulyaeva and Bilitza, 2012]. The inaccurate representation of this part of the ionosphere in both models may also contribute significantly to TEC data‐model discrepancies. According to Bilitza et al. [2006], the truthful representation of fountain effect in the equatorial region in almost all the topside models is still a major challenge for topside modeling. This may contribute significantly to the poor performance of both models within the equatorial region. The result obtained showed that the IRI model, in particular, the NeQ and IRI‐01 Corr options, generally performed better than the IRI‐Plas at stations in the equatorial region. This may be attributed to whether the equatorial features like the high altitudes of the equatorial ionosphere and the equatorial ionospheric transport process have been adequately addressed in the two topside options.
In addition, the poor performance of the IRI‐Plas model within the equatorial region may also be attributed to the inaccurate prediction of the plasmaspheric contribution to TEC in the region. The plasmaspheric contributions to the GPS‐TEC have been reported to vary spatially and temporally [Satya Srinivas et al., 2013; Balan et al., 2002; Klimenko et al., 2014]. For example, plasmaspheric contribution to TEC has been reported by Satya Srinivas et al. [2013] to reach up to 30% at the equatorial latitudes during the daytime, while Klimenko et al. [2014] reported a nighttime maximum contribution of 85% and a daytime contribution of 40% at the equator during the winter in the year 2009 (a period of extreme solar minimum condition). Balan et al. [2002] reported a contribution of about 12% during the daytime and 60% during the nighttime over Japan. The plasmaspheric contribution to TEC has also been found to decrease with increase in latitude and altitude [e.g., Lunt et al., 1999; Klimenko et al., 2014]. For example, Yizengaw et al. [2008] and Klimenko et al. [2014] reported a higher plasmaspheric contribution to TEC at the equatorial latitudes than in other latitudes. This was attributed to longer receiver satellite path length in the equatorial region compared to other latitudes. This may account for the improved performance of both models, particularly the IRI‐Plas model, outside the equatorial region. All these point to the fact that the plasmaspheric contribution to GPS‐TEC depends on several factors such as solar activity, season, latitude, altitude, and local time [Klimenko et al., 2014], and detailed knowledge of its variation over the region may be vital. It is therefore suggested that the structure and the dynamics of the plasmaspheric electron content should be investigated at different space weather conditions over the region. Results from such investigation will be useful to improve on the performance of existing plasmasphere models in the region or to develop new ones.
5 Conclusion
We have investigated the performance of the IRI and IRI‐Plas models in terms of TEC prediction over eight stations located in the Southern African equatorial and low‐latitude region. The diurnal and seasonal structures of TEC predicted by both models followed fairly well with the observed structure. Generally, both models overestimate and underestimate TEC during the daytime and the nighttime. In most cases, the IRI‐Plas performed better than the IRI model in the months and seasons at the time the three options of the IRI model underestimate TEC during the daytime. This has been attributed to the height limitation of the IRI model. Overall, the best predictions by both models were recorded during the September equinox (SEQU) at stations outside the equatorial region while the worst are obtained in June solstice, particularly in the equatorial region. The prediction errors of both models generally decrease with increasing latitudes, indicating that both models predict TEC better outside the equatorial region. In general, the data‐model divergence of TEC is most significant during the daytime and the nighttime at stations in the equatorial region. On the other hand, the data‐model convergence is most pronounced during the nighttime at stations outside the equatorial region in most of the months. The TEC data‐model offset has been attributed to the height limitation of the IRI model, the inaccurate predictions of the electron density profiles, and the plasmaspheric contribution to TEC in the region. More studies are required to determine the contributions of each of these factors to data‐model discrepancy.
Acknowledgments
The authors are grateful to the IRI working group for their efforts in improving the IRI model and for making it available freely to the international community from the link: http://modelweb.gsfc.nasa.gov/ionos/iri.html. The authors would also like to thank the International GNSS Service (IGS) team for the GPS data (available at ftp://garner.ucsd.edu.) and the IONOLAB group for implementing the IRI‐Plas model and making it available for public use and can be accessed at www.ionolab.org. One of the authors (Adebiyi, S. J.) thanks F. Arikan (Hacettepe University, Beytepe, Ankara, Turkey) for providing useful information on the online computation of IRI‐Plas 2015 model products.
Notes :
- 1 The numbers in bold indicate the value of the model with the lowest prediction error.
- 2 The numbers in bold indicate the value of the model with the lowest prediction error.
Number of times cited: 1
- Umut Sezen, Tamara L. Gulyaeva and Feza Arikan, Performance of Solar Proxy Options of IRI‐Plas Model for Equinox Seasons, Journal of Geophysical Research: Space Physics, 123, 2, (1441-1456), (2018).





